reptile7's JavaScript blog

Saturday, February 25, 2023
Memory Coda and Most of the
scie( ) Function StoryBlog Entry #418
I've got a bit more to say about the memory business before moving on...
Toward a more normal memory
Like the Super Calculator and its and keys, my handheld Casio fx-85v calculator has a key for basic memory input, although the two calculators have different post-memory behaviors, namely,
upon inputting a first number and copying it to memory and then inputting a second number,
the Casio overwrites the first number in the display field with the second number -
pressing and then and then gives a 7 display - whereas
the SC appends the second number to the first number in the total field -
pressing and then and then gives a 97 total value.
I prefer the Casio behavior to that of the SC and would sync the latter with the former via a meminput global boolean flag as per our approach to an M+ capability in the previous post. Accordingly, the
more( ) function that controls the total display becomes:var meminput = 0, memplus = 0;
function more(obj, where) {
/* If the meminput or memplus flag was switched to 1 by the getinput( ) function, then a new input replaces a preceding input. */
if (where.value == "" || where.value == "0" || meminput || memplus) where.value = obj;
/* If both flags are 0, then a new input is appended to a preceding input. */
else where.value += obj;
/* meminput or memplus must be turned off for a new input having more than one character. */
if (meminput) meminput = 0; if (memplus) memplus = 0; }• You might prefer the original SC behavior if you wanted to do some arithmetic on the first number after memorizing it.
• Not mentioned previously: I named the M+ flag memplus and not mem+ because a JavaScript identifier cannot contain a + symbol.
My Casio also has an key and an M- function that is accessed by SHIFT-ing the key, and a sequential use of the key, the key, and the M- function clearly indicates that they all interact with a common hidden field.
In the previous post we converted the SC's key to an key
but if we alternatively add a new key and leave the key in place
then both controls will act on the memory2 field à la the Casio and
we can similarly add a new key that does so as well.
function getinput(func) { ...
if (func == "mem-") { memminus = 1; return mem(mode, a, c); } ... }
var meminput = 0, memplus = 0, memminus = 0;
...updated mem( ) and more( ) code...
<button type="button" onclick="getinput('mem-');"> M- </button>As a power of 10
Just above the SC's Memory section - at the top of its tables[2] table - is a Scientific Notation section.
Scientific Notation:
The key calls on a
scie( ) function to express a standard form number in scientific notation, e.g., it'll convert 2023 to 2.023*10^3. The "standard form" and "scientific notation" number descriptors evidently have different definitions in the US and in the UK - I'll use their American definitions in the discussion that follows. Complementarily, the key calls on an unscie( ) function that solicits the user for the "decimal" (coefficient) and the "power that is given to 10" (exponent) of a scientific notation number and then outputs the corresponding standard form number.Standard to scientific
The
scie(mode, obj) function is calledand equipped with mode = 1|0 and obj = document.mainform.total arguments
by the
getinput(func) function in the usual manner.(See the complete, unabridged SC code for the full details.)
A switched-on mode effects the display of an
alert( ) help pop-up whose message reads:Scie is [a] cool function that allows you to convert any given number into scientific notation. The format of the answer is as follows: Ex: input:120, output:1.2*10^2, would be 1.2 multiplied by 10 to the second power.
Next, the user is
prompt( )-queried for a number to express in scientific notation - you know the drill:if (obj.value != "" && obj.value != "0") {
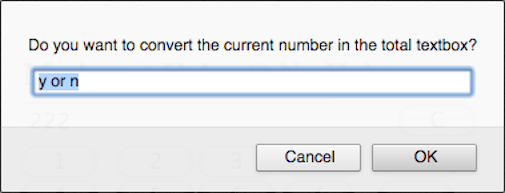
aa = window.prompt("Do you want to convert the current number in the total text box?", "y or n");
if (aa == "y") a = obj.value;
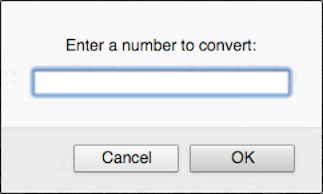
else a = window.prompt("Enter a number to convert:", ""); }
else a = window.prompt("Enter a number to convert:", "");The standard form number input is given an a identifier
and is converted into scientific notation by the following code:
var b = 0;
while (a > 10) { // Divide by ten until variable is no longer greater than 10
a /= 10;
b += 1; }A while loop iteratively divides a by 10 until a is less than or equal to 10. Meanwhile, a b counter counts up the number of divisions and will subsequently serve as the exponent in the final output.
Lastly, a
doit(a + "*10^" + b, obj) commandconcatenates a, *10^, and b
and the resulting string and obj are shipped off to the
doit( ) function,which loads the former into the latter.
Per the No offshoring needed subsection of the previous post, the
doit( ) action is actually unnecessary:an
obj.value = a + "*10^" + b assignment works just as well.Starting a scope notes
If a is itself a positive integer power of 10, say 100000, then the while divisions will stop when a hits 10 and the output will be 10*10^4 versus the 1*10^5 output we would want: adjusting the while condition to
a >= 10 solves this problem.For as less than 10,
the while condition returns false from the get-go,
b stays at 0,
and the output has the form a*10^0,
which is what we would want
for positive as ranging from 1 up to but not including 10
and for negative as ranging from -1 down to but not including -10
but is not what we would want
for positive and negative as between 1 and -1
and for negative as less than or equal to -10.
We can accommodate all number as and also weed out nonnumber as with the following code:
var b = 0;
while (! isNaN(a)) {
if (a >= 10 || a <= -10) { a /= 10; b += 1; }
else if (a < 1 && a > 0 || a < 0 && a > -1) { a *= 10; b -= 1; }
else break; }
if (a == 0) { obj.value = 0; return; }
if (isNaN(a)) { window.alert("Please input a number."); obj.value = 0; return; }
obj.value = a + "*10^" + b;For positive and negative as between 1 and -1, a is iteratively multiplied by 10 and b is decremented until a rises above 1 or falls below -1, e.g., 0.000017 (the acid dissociation constant for acetic acid) is converted to 1.7*10^-5.
When a reaches its final value, the
! isNaN(a) condition is still true, so the loop is terminated with a break statement, otherwise it would run indefinitely.The a value can be 0 or the empty string
if the user respectively enters 0 into or leaves blank
and s the
prompt( ) box that pops up if either(a) the total field holds 0 or is blank initially
or (b) the user does not answer y to the
prompt( ) query.(The preceding images are Preview-enlarged screen shots that were originally taken when using Firefox.)
In these cases - given that
"" == 0 returns true1 - the else if (a == 0) clause resets the total value to 0 and ends the scie( ) function via a return statement.FYI: 0 is a
special case [that] does not have a unique representation in scientific notation, i.e., 0 = 0 × 100 = 0 × 101 = ...
By nonnumber as I specifically mean any and all a strings for which
Number(a) returns NaN. A nonnumber a value is converted accordingly to NaN for the original a > 10 while condition1, which in that case returns false as when NaN is one of the operands of any relational comparison (>, <, >=, <=), the result is always false, quoting Mozilla, and the output again has the form a*10^0. We have seen previously that nonnumber strings include not just alphabetic text like Hello World but also legitimate mathematical expressions like 123*(456+789), which should be
eval( )ed with the key before being fed to the scie( ) function. As detailed above, my code flags nonnumber as and then pops up a Please input a number alert, resets the total value to 0, and returns.1
When comparing a string with a number, JavaScript will convert the string to a number when doing the comparison. An empty string converts to 0. A nonnumeric string converts to NaN[, which always causes a false return]- see the Comparing Different Types section of W3Schools' JavaScript Comparison and Logical Operators page.
The null thing
Up to this point I have negligently not said anything about what happens if the user cancels the various SC function prompts, and now is a good time to do so. Clicking the button on a
prompt( ) box returns the primitive value null (not "null" as a string). Number(null) returns 0 and isNaN(null) relatedly returns false, and the null value that is returned by canceling the SC functions' 'Enter a number to do X' prompts2 does behave like 0 for the mathematical operations that follow those prompts, e.g., Math.cos(null) returns 1 and Math.log(null) returns -Infinity.2A user usually first sees a
'Do you want to use the current number in the total text box to do X?' prompt,
whose cancelation leads to an 'Enter a number to do X' prompt -
see, e.g., this code given earlier.
For the
scie( ) function, then, canceling the "Enter a number to convert:" prompt (vide supra) gives an a = nullwhose
a > 10 while test returns false and
that is outputted as null*10^0. It would be better to intercept that null as we did the empty string and other nonnumber as, yes?The a = null gets through the modified
! isNaN(a) while gate but there is some strangeness in null vs. 0 comparisons in thatnull >= 0 and null <= 0 both return true but
null == 0 itself returns false.
Stack Overflow has a Why 'null >= 0 && null <= 0' but not 'null == 0'? page at which commenters Michael Liquori and/or Christian C. Salvadó link to relevant sections in the ECMAScript-262 Edition 5.1 specification -
specifically, 11.8.5 The Abstract Relational Comparison Algorithm (ARCA) and 11.9.3 The Abstract Equality Comparison Algorithm (AECA) -
that together with other sections in the specification provide detailed procedures for carrying out such comparisons. In brief, here's what happens:
(R) For the null >= 0 and null <= 0 relational comparisons, null is converted to +0 (yes, positive zero) via a
ToNumber(null) operation (this also occurs for the null > 10 relational comparison). The mathematical value of +0 is simply 0 (see the eighth paragraph of this specification section), and the ARCA tests if the left-hand +0 → 0 is less than the right-hand 0 and returns false, which is subsequently adjusted to true for the >= operator and for the <= operator.(E) For the null == 0 equality comparison, the AECA leaves null alone and returns false - that's it.
Anyway, getting back to the interception of an
a = window.prompt("Enter a number to convert:", "");-canceled null in the scie( ) function, it follows that an a == 0 test isn't going to do the trick. A simple solution is at hand, however; we can trap null (or the empty string or 0 while we're at it) by Number( )izing a before comparing it to 0:if (Number(a) == 0) { obj.value = 0; return; }An archival aside:
We first discussed the
prompt( ) method of the window object, and the → null return, in Blog Entry #11, which dates to my early blogging days and which I admit I find somewhat painful to read today. My choice of links for that entry provides a snapshot of the thrashing around I did documentation-wise prior to discovering Netscape's and the W3C's reference materials. Most but not all of those links had been dead for a while when I began writing the current post; I've recently gone to the trouble of repairing the dead ones, so you can go check out The Prompt( ) Method for yourself if you would like a pristine taste of my 'humble beginnings'. ☺More ECMAScript specification notes, in the name of completeness
Without getting into its grammar productions, the 9.3.1
ToNumber Applied to the String Type section covers the "" == 0 and nonnumeric string → NaN situations that were addressed earlier:If the grammar cannot interpret the String as an expansion of StringNumericLiteral, then the result of ToNumber is NaN.The MV [mathematical value] of StringNumericLiteral ::: [empty] is 0.
In actuality, a relational comparison with a NaN operand initially returns undefined, which is subsequently adjusted to false.
The ECMAScript-262 Edition 5.1 specification went live in June 2011; the current ECMAScript specification is located at
https://tc39.es/ecma262/.
In our next episode we'll deal with two more
scie( ) function issues:(1) Do you like the 2.023*10^3 output format? No? I don't either. Let's see if we can change it to 2.023×103, shall we?
(2) I ran 12345 through the
scie( ) function and got 1.2345000000000002*10^4. Huh? What's with all those trailing digits? We'll get this worked out.Sunday, January 01, 2023
I Do Remember, I Do Recall
Blog Entry #417
Let's get back in the saddle and lasso the next Super Calculator item on the agenda, that being the Memory section.

Neither Jamie Beyore's Another Great Science Calculator nor Saries's Rainbow Calculator has a memory facility (actually, most JavaScript calculators don't have one), so this will be new territory of sorts for us.
I can't recall ever owning a calculator that had more than one memory field: the SC has two of them. The SC's Memory keys work with a pair of hidden controls for storing values or expressions to be remembered.
<!-- These inputs are at the very end of the mainform form. -->
<input type="hidden" name="memory1">
<input type="hidden" name="memory2">
</form>Memory in
The and keys load the total value into the memory1 and memory2 fields, respectively, via a common
mem( ) function.function getinput(func) {
var a = document.mainform.total;
var b = document.mainform.memory1;
var c = document.mainform.memory2;
var mode = document.mainform.mode[0].checked ? 1 : 0; ...
if (func == "mem1") { return mem(mode, a, b); }
if (func == "mem2") { return mem(mode, a, c); } ... }
// obj is the user input field, where is the hidden field
function mem(mode, obj, where) {
if (mode == 1) { window.alert("Pressing the memory button allows you to save the current number in the total text box for later use. You can recall the remembered number by pressing the Rcl button."); }
where.value = obj.value; }
<td><b>Memory:</b><br>
<input type="button" value=" M1 " onclick="getinput('mem1');">
<input type="button" value=" M2 " onclick="getinput('mem2');"> ...M1/M2 deconstruction
Clicking the push button calls the
getinput( ) functionand passes to the
getinput( ) function a 'mem1' string(versus a function reference as per the SC functions we've discussed previously)
that is assigned to the func parameter of the
getinput( ) function.Next, the total, memory1, and memory2 fields (more precisely, the Text and Hidden object reflections of those fields) are variabilized as a, b, and c, respectively, and then
the mode help flag is set to 1 if we wantHelp or to 0 if we preferNo Help.
A func == "mem1" comparison subsequently triggers the
mem( ) function, to which is passed mode, a, and b, which are assigned respectively to the mode, obj, and where parameters of the mem( ) function.If mode is 1 (its initial value), then a
Pressing the memory button allows you to save the current number in the total text box for later use. You can recall the remembered number by pressing the Rcl button.
alert( ) message pops up.Lastly, the obj/total value is copied to the where/memory1 field.
Things go in a corresponding way with the button, the differences being that
(a) a 'mem2' string is passed to the
getinput( ) function,(b) a func == "mem2" comparison triggers the
mem( ) function, and(c-d) the c Hidden object is passed to the
mem( ) function and then assigned to the where mem( ) parameter.where.value scope
A conventional calculator memory facility - check the calculator at https://www.online-calculator.com/ -
allows the user to store a number. With the SC, we can do that too of course
although we can also memorize a larger expression like 2*(3+4); as the total field is not readonly, moreover, we can even input and save something like Math.pow(2, 7).
• How long and involved can those numbers and expressions be? The total field does not have a maxlength setting, suggesting that there is no limit to the number of characters that can be loaded into the total, memory1, and memory2 fields.
More specific help
Although the and keys have the same help message, it is simple enough to differentiate the message for each key.
function mem(mode, obj, where) {
var memID = where.name.substring(6, 7);
if (mode) window.alert("Pressing the M" + memID + " key allows you to save the displayed value (number or expression) in a hidden memory" + memID + " field. You can redisplay the remembered value by pressing the Rcl" + memID + " key.");
where.value = obj.value; }The 1 or 2 differentiator at the end of the hidden input name is
substring( )-extracted and then stored in a memID variable, which is subsequently deployed in a modified help message. For the key, the new message is:Pressing the M1 key allows you to save the displayed value (number or expression) in a hidden memory1 field. You can redisplay the remembered value by pressing the Rcl1 key.
Besser, ja?
Out of storage
For their part, the Memory section's and keys
<input type="button" value=" Rcl1 " onclick="getinput('rcl1');">
<input type="button" value=" Rcl2 " onclick="getinput('rcl2');">indirectly call on
a
getinput( )-gated rcl( ) functionfunction getinput(func) {
/* The a, b, c, and mode variables are defined above. */ ...
if (func == "rcl1") { return rcl(mode, b, a); }
if (func == "rcl2") { return rcl(mode, c, a); } ... }
// obj is the hidden field, where is the user input field
function rcl(mode, obj, where) {
if (mode == 1) { window.alert("Rcl is a neat function that works with Memory. It recalls and gives you the number you saved in the coresponding [sic] memory."); }
if (obj.value == "") { more("", where); }
else { more("(" + obj.value + ")", where); } }and the
more( ) functionto respectively send the memory1 and memory2 values to the total field.
rcl( )/more( ) possibilities, plus some code-tighteningDeconstruction-wise, let's go straight to
rcl( )'s post-help statements; I trust you can handle everything else up to that point. Here's the skinny on what can happen:(i) If there's nothing in the memory1|memory2 field and the total value is 0 or the empty string, then the total value is set to the empty string, i.e., the total field is blanked.
(ii) If there's nothing in the memory1|memory2 field and the total field holds some nonzero value, then the empty string is appended to the total value, and the total value stays the same.
(iii) if there's something in the memory1|memory2 field and the total value is 0 or the empty string, then the total value is set to the memory1|memory2 value surrounded by parentheses.
(iv) if there's something in the memory1|memory2 field and the total field holds some nonzero value, then the memory1|memory2 value surrounded by parentheses is appended to the total value.
Got all that? Now, if the memory1|memory2 field is empty, then why are we sending anything to the total field via the
more( ) function? Can't we just return for the (i) and (ii) cases and be done with it? Actually, yes, we can do that. But given that the rcl( ) function is itself equipped with an object reference argument for the total field, we don't need to outsource the (iii) and (iv) cases to the more( ) function either. The rcl( ) function can take care of the whole shebang all by its lonesome:function rcl(mode, obj, where) {
var memID = obj.name.substring(6, 7);
if (mode) window.alert("Clicking the Rcl" + memID + " key recalls and displays the value (number or expression) that you saved via the M" + memID + " key.");
if (obj.value == "") return;
else if (where.value == "0" || where.value == "") where.value = obj.value;
else where.value += "(" + obj.value + ")"; }For the (iv) case, if you would rather just replace the total value with the memory1|memory2 value - this is what happens with the key on most calculators, in my experience - then the post-help part of the preceding function can be simplified to:
if (obj.value == "") return;
else where.value = obj.value;No offshoring needed
At this point I should note that thirteen of the seventeen
getinput( )-gated functions secondarily call on the more( ) and/or doit( ) functions to load a value into the total field (besides rcl( ), see the power( ), squareroot( ), and sine( ) functions, e.g.). The getinput( ) function passes the var a = document.mainform.total; object reference to all thirteen of these functions, and therefore their various calculation returns can be sent 'in house' to the total field if desired.Memory addition
In the Memory subsection of the Operational overview section at the end of the first post of this series I parenthetically said that and are
M+keys. A conventional key on a standard calculator is used to add a series of numbers in a hidden field, however, and the aforedetailed
mem( ) function can't do that. Suppose we want to make a standard M+ key. What changes would be necessary?M2 → M+
We can write a separate, dedicated function for our M+ key, or not: we can continue to make use of the
mem( ) function if the M+ process can be toggled on and off as needed, and a global boolean flag is a handy tool for doing just that.In the code below,
the memplus variable is globally initialized to 0
and is toggled to 1 in the
getinput( ) function right before the mem( ) calland in the
mem( ) function the switched-on memplus green-lightsthe display of an M+ help message and
the addition of numberified* memory2 and total values in the memory2 field. (*The unnumberified values would be concatenated.)
function getinput(func) { ...
if (func == "mem+") { memplus = 1; return mem(mode, a, c); } ... }
var memplus = 0;
function mem(mode, obj, where) {
if (mode) {
if (memplus) window.alert("Pressing the M+ key enables you to add a series of numbers in a hidden memory field. You can display the hidden sum by pressing the Rcl2 key.");
else /* alert( ) for the remaining key, if present */ }
if (memplus) where.value = Number(where.value) + Number(obj.value);
else where.value = obj.value; // As per the original function }
<input type="button" value=" M+ " onclick="getinput('mem+');">The
where.value = Number(where.value) + Number(obj.value); operation takes care of normal numeric string inputs. We noted earlier that we can input larger expressions into the memory1/memory2 fields. If we want to M+ such expressions - either to themselves or to normal numbers - we have a couple of options:(1) We can
eval( ) each expression to a number before we remember it and subsequently add our M+ addendsvia a
where.value = Number(where.value) + eval(obj.value); operation.(2) More generally, we can remember each expression as is and insert a + symbol between each pair of M+ addends so that when the whole thing is recalled it can be
eval( )ed in one go with the key:if (where.value == "") where.value = obj.value; // For any initial addend
else if (! isNaN(where.value) && ! isNaN(obj.value)) where.value = Number(where.value) + Number(obj.value); // If both addends are numbers
else where.value = where.value + "+" + obj.value; // If at least one addend is not a numberThe former approach is good for any and all legitimate mathematical expressions but will balk at (throw an error for) an input like Hello World. The latter approach will handle any expression under the sun without batting an eye.
We're not done yet. Consider the M+ addition of 9 and 13 as carried out by the aforecited Online-Calculator.com calculator.
We press the 9 key, thereby entering a 9 into the user input field, and then the M+ key.
Pressing the 1 key for 13's tens place digit overwrites the 9 in the user input field with a 1; pressing the 3 key for 13's ones place digit appends a 3 to the 1 in the user input field.
We press the M+ key a second time. Pressing the MR key now outputs the M+ sum, 22, to the user input field.
For doing this back at the SC, clearing the 9 M+ addend without clearing the starting 1 of the 13 M+ addend requires us to tweak the
more( ) function in a couple of ways:function more(obj, where) {
if (where.value == "" || where.value == "0" || memplus) where.value = obj;
else where.value += obj;
if (memplus) memplus = 0; }When the memplus flag is on, a new total value (obj, admittedly a poor choice of variable names in this context) replaces a preceding total M+ value.
If the new value consists of more than one character AND
we're going to input those characters one by one via the SC's number/operator keys AND
we don't want each character to be replaced by the following character during the input process,
then it is necessary to turn memplus off at the end of the function once the zeroth character is in place.
Subtraction action
If your calculator has an M+ key, then it probably also has an M- key for subtracting a series of numbers from a minuend in a hidden field. Adding an M- functionality to the SC is no more difficult than changing the + operators in the above M+ code to - operators. That said, if we want the SC to have both an M+ key and an M- key in addition to the original and/or keys, then it may well be a good idea to deploy discrete M+, M-, and Min (memory input) hidden fields and functions just to keep it all straight and readable.
The eraser
Finally, clicking the Memory section's key
<input type="button" value=" MC " onclick="getinput(mc);">calls (indirectly via the
getinput( ) function, as per usual) an mc( ) function that empties the memory1 and memory2 fields by setting their values to empty strings.function getinput(func) { ...
if (func == mc) { return mc(mode, b, c); } ... }
function mc(mode, obj1, obj2) {
if (mode == 1) { window.alert("Memory Clear is an easy little function that erases the values of both memorys [sic]."); }
obj1.value = "";
obj2.value = ""; }I don't think we need any commentary for this one.
We're down to the last few SC keys and functions - we'll cover the Scientific Notation section in the next post.
Sunday, August 29, 2021
Summer 2021 Updates
Blog Entry #416
We will return to our Super Calculator discourse shortly, but we have some administrative business to deal with first...
The new and unimproved HTML Goodies
A few months ago - on or about 1 May - the HTML Goodies site was redesigned; I don't know if the current HTML Goodies owner, TechnologyAdvice, did the redesigning or not.
Some quick HTML Goodies JavaScript history before we go any further:
• The introductory JavaScript Primers were in place in late 1998.
• The JavaScript Script Tip series ended in mid-2000.
(A final "Post the Tables" tip was posted externally on 31 August 2000.)
• The Beyond HTML : JavaScript sector was a work in progress when I began blogging in March 2005, and remained so as its own entity, adding and removing tutorials over the years, until the recent redesign.
• The JavaScript Keyword References came on line with a 15 February 2005 site redesign.
• Most recently, the JavaScript Frameworks sector got going in July 2011.
The new HTML Goodies features a single Javascript (sic) sector that provides links to about 550 pages of content, not all of which is JavaScript-related. The /javascript/ page displays eight links in a
<div> at a time; it is necessary to repeatedly click a button below the div to load successive sets of links into the div. The links run in roughly reverse chronological order although things get a bit chaotic upon hitting the pre-2003 Joe Burns-era material about two-thirds of the way in.N.B. For tutorials that run longer than one page, only the first page remains, e.g., "How to Create a JavaScript Animation", see the intact tutorial here.
Significantly, the resources of the Javascript and other site sectors have all been given new URLs; as a result, most of this blog's many links to HTML Goodies pages are now dead. The interpage links at the site's portal pages - "HTML Goodies – The Master Page", "JavaScript Primers – Table of Contents", the Script Tips index, etc. - are similarly kaput. Wunderbar, eh? As you can imagine, this sort of thing really makes my day.
In fairness to TechnologyAdvice, I should point out that the site URLs were changed with the aforementioned 15 February 2005 redesign as well.
Consider the JavaScript Primer(s) #1, whose original URL was
http://www.htmlgoodies.com/primers/jsp/hgjsp_1.html;
on 15 February 2005 its URL changed to
http://www.htmlgoodies.com/primers/jsp/article.php/3478211
whereas today its URL is
https://www.htmlgoodies.com/javascript/javascript-primers-1/.
Ideally, the site URLs would not have changed in 2005; moreover, I'll concede that javascript-primers-1 is a much better file identifier than 3478211 is. Having said this, I think that TechnologyAdvice should have stuck with the 15 February 2005 URLs as they had been in use for more than fifteen years.
Support directory notes:
The /legacy/beyond/javascript/ directory
holding code and demos for the Script Tips and for the pre-2003 Beyond HTML : JavaScript tutorials
is still live as of this writing.
The /img/ directory
holding images plus some code (mostly .js scripts) and the odd demo
is gone.
Java/JavaScript Goodies, the Internet Archive, and .txt scripts
In the last few months of 2013
I concluded my coverage of the JavaScript material at HTML Goodies
and started work on the Java Goodies JavaScript Repository that Joe Burns curated in the late 1990s.
The Java Goodies project was originally an htmlgoodies.com/javagoodies/ part of HTML Goodies but at some point in 1998 was spun off as a separate javagoodies.com site. Joe pulled the plug on Java Goodies/javagoodies.com in late 1999/early 2000, although most of the repository content is still accessible via the Internet Archive. Format-wise, the Java Goodies script code pages are in most cases plain-text .txt files.
Nearly all of the Java Goodies scripts also appear in the online Appendix D companion to the JavaScript Goodies book that Joe wrote with Andree Growney. The htmlgoodies.com/JSBook/appD.html collection of scripts used to be part of the live HTML Goodies site, but the /JSBook/ directory was dropped with the 1 May 2021 redesign.
Some of the Java Goodies scripts were not 'crawled' by the Internet Archive way back when but were present in the Appendix D collection, and I would link to the latter as appropriate. In 2016 or 2017, extraneous HTML started showing up in the Java Goodies scripts - I doubt that this was a gradual process, but I can't tell you exactly how it played out as it happened while I was repairing the blog potholes caused by my severing ties with EarthLink (see here, here, here, and here) - anyway, it was no longer possible to Select All ⌘A and Copy ⌘C the original, unadulterated scripts at the archived javagoodies.com as it was at the live /JSBook/ directory, so I left the former behind and subsequently worked from the latter.
As noted a moment ago, however, those JavaScript Goodies scripts aren't live any longer; like their Java Goodies counterparts, they can be accessed via the Internet Archive and are now defiled with extraneous HTML. But wait ... as it happens, a very few of these scripts do appear as they should appear - you see only the script code plus an overlying Internet Archive navigation widget at the top of the page, and nothing else - so I decided to take a closer look at them in order to figure out what was going on rendering-wise.
One of the displays-as-it-should scripts is the "How Many Days Until Christmas?" xmas.txt script that we discussed in Blog Entry #308. Check over the https://web.archive.org/web/19981206200117/http://www.javagoodies.com/xmas.txt crawl page and its underlying source. (Actually, a .txt page shouldn't have a separate source like an .html page does, but leave that aside for the time being.) The source
<body> features a <div>/<table> structure that codes the aforementioned navigation widget.
What you won't see in the source is the original "How Many Days Until Christmas?" script code; in practice, the script code on the crawl page comes from an external page (view it here) that is fetched and framed by an
<iframe id="playback" ...>. (Maybe I'm missing something, but I see no need to externalize the script code given that the navigation widget has a fixed positioning.)Anything else? Filling things out, the source also sports
a couple of
<link>s to external style sheets,seven
<script>s (some with inline code, some that point to .js files) spread across the <head> and <body>, andfive
<!-- comments -->s that annotate the navigation widget.That the crawl page is a .txt document is significant
in that if we were viewing it on the desktop we would see
the navigation widget code rather than the navigation widget itself,
the playback iframe code rather than the "How Many Days Until Christmas?" script code, and
the aforedetailed
<link>s, <script>s, and <!-- comments -->s.At the Internet Archive, however, we see the crawl page as an HTML document, its .txt extension notwithstanding, because it is served to us with a text/html Content-Type, as can be confirmed by running the crawl page URL through Rex Swain's HTTP Viewer.
In contrast, check out the 8 October 1999 https://web.archive.org/web/19991008153633/http://www.javagoodies.com/makepassword.txt crawl page that I linked to for the "Make Me A Password" script that we discussed in Blog Entry #305: this page is served to us with a text/plain Content-Type, as one would expect for a .txt file.
The original "Make Me A Password" script code is present on the aforecited /makepassword.txt crawl page (the playback iframe is gone) and is now intertwined there with the same sort of supporting code
that is present in the source of the /xmas.txt crawl page and
that would not be visible on a text/html page;
the supporting code includes code for a navigation widget that would link us to a second, 2 May 1999 /makepassword.txt crawl page if it were rendered, which it is not.
As stated above, the /makepassword.txt situation is the rule and the /xmas.txt situation is very much the exception as regards the Java/JavaScript Goodies scripts, and I don't know the reason for that. The reason may not be deliberate: maybe the Internet Archive didn't text/plain the exceptions because of a glitch of some sort. In any case, let me sum up by saying that if the Internet Archive is going to add its own HTML to a set of related .txt or other text files (or to standalone text files that have only been crawled once), then it should always serve those files as text/html files.
I can understand why Joe posted the Java Goodies scripts as .txt files rather than as .html files:
in choosing the former there was no need
to literalize
< and > characters as < and > respectively orto add elements (e.g.,
<nobr>, <br>) that preserve the formatting of the code.Joe subsequently formed and posted the Script Tips scripts as .html files; the Internet Archive's crawls of these scripts are linked by navigation widgets and are cleanly readable - e.g., see here and here.
This brings us back to the Super Calculator script. The https://www.htmlgoodies.com/JSBook/supercalc.html SC demo/description page is history, but at least it's archived history. I can't really say the same for the matching http://www.htmlgoodies.com/JSBook/supercalc.txt SC script code page, however; although this page is history too and has been crawled a bunch of times by the Internet Archive, the archived crawls are not clean copies of the original page but, per the /makepassword.txt example above, are adulterated with (unrendered) navigation widget code, two
<link>s to style sheets, etc.A user shouldn't have to prune away a bunch of stuff to get to a script, so perhaps I should get back into the practice of posting these scripts myself. With no further fanfare, then, here is the original supercalc script code:
I've placed the code in a textarea box
<textarea id="scTextarea" name="myTextarea" cols="" rows="" style="width:95%;height:250px;">...SC script code...</textarea>rather than in a div as I used to do.
Textarea advantages vis-à-vis a div
On the user's part:
(1) The user can click on the textarea box and Select All ⌘A the code in one go; it's not necessary to mousically select the code from start to finish.
(2) If the textarea content hasn't been readonly-ed, then the user can edit the code in place and then select and copy it, and you certainly can't do that with a div.
On my part:
(3) The textarea element's Text/#PCDATA content model* means that I don't have to convert
<s to <s and >s to >s.(4) White space - newlines, empty line boxes, indentation - in an external source is preserved when the source is pasted into a textarea box (however, a
white-space:pre;-styled div will also preserve white space).*Content model fallout:
(i) I can't mark up the code with the
<code> element as I normally would.(ii) Remember those
s that push the by Tom Richardson Jr. authorship credit to the right? Left untouched, they are rendered as spaces in the textarea box just like they are on the page: to print them out as s in the box, it is necessary to literalize the &s, e.g., &nbsp;&nbsp;&nbsp;...Other supercalcs, in the name of completeness
I found a couple of slightly modified, unrelated-to-Java/JavaScript Goodies copies of the supercalc code via a relevant Google search.
https://www.angelfire.com/mo/chaset/calculator.html
- this page dates to 1998 or so, Angelfire is still around but is now owned by Lycos, check the source for the code
- adds
<html> and <head> and <body> markup, adds a <title>Calculator</title>- places the
<script> just inside the <body>, which is OK, but does not delete the original </head> end tag that immediately follows the </script> end taghttps://web.archive.org/web/20000519100508/http://www.htmlpoint.com/jscript/calcolatrici/calcolatrici04.htm
- displays the code in a textarea box on the page, maybe I should do that from now on
- adds
<html> markup, inserts a <head> start tag before the <script>, adds <body> markup and sets the bgcolor to #ffffff- quotes all attribute values, tweaks a couple of numerical settings
- the two links have extraneous
tppabs attributes that are set to the original href URLs (this isn't standard, it's some sort of offline browsing thing, I'm not familiar with it), they also have href attributes that point to an http://www.htmlpoint.com/jscript/tppmsgs/msgs0.htm page that is no longer availableFriday, July 02, 2021
Reflected Through Zero
Blog Entry #415
So, what's left in our Super Calculator odyssey?
Some of the SC's remaining features - specifically, the key and the Memory keys - are normal calculator fare
although some of them - specifically, the Scientific Notation, Finding "x", and Fractions keys - are kind of odd;
my inclination is to discuss the former in detail
and skim through the latter.
Going from one side of the number line to the other
Nestled between the SC's and keys
is a key
<input type="button" value=" +/- " onclick="getinput(negpos);">that is indirectly bound to a
negpos( ) functionfunction getinput(func) {
var a = document.mainform.total; ...
var mode = document.mainform.mode[0].checked ? 1 : 0; ...
if (func == negpos) { return negpos(mode, a); } ... }
// Change the sign of any given number
function negpos(mode, obj) {
if (mode == 1) { window.alert("+/- allows the [sic] you to convert a negative(-) number to a positive(+) and a positive number to a negative. And then it puts it in the total text box with any other number that is already in there."); }
obj.value *= (-1); }that converts the total field's value to its additive inverse by multiplying it by -1.
Unlike the SC's exponentiation and trigonometry functions, the
negpos( ) function does not trouble the user with a "Do you want to use the current number in the total text box for this operation?"-type prompt( ),nor does it call on the
doit( ) and more( ) functions to load the new obj.value into the total field.The
negpos( ) help message's second sentence seems to say that the new total value is appended to the starting total value, which does not happen: the former replaces the latter.If the initial obj.value can be converted to a number for the
* (-1) multiplication, then all is well, but if not, then the negpos( ) output is NaN - more on this below.Other inversions
Jamie Beyore's Another Great Science Calculator has a key but not a key.
Saries's Rainbow Calculator has a key and a key; the former is directly bound to a
change( ) function, which I did not discuss in Blog Entry #74, so let's take a quick look at it now:function change( ) {
var temp = document.calculator.text.value;
if (temp.substring(0, 1) == "-") {
document.calculator.list.value = "";
document.calculator.text.value = 0 - document.calculator.text.value * 1; }
if (temp.substring(0, 1) != "-") {
document.calculator.list.value = "";
document.calculator.text.value = "-" + temp.substring(0, temp.length); } }
<form name="calculator"> ...
<input name="list" type="hidden"> <!-- The list field serves no purpose. -->
<input type="text" name="text" value=""> ...
<input type="button" value=" +|- " name="sign" onclick="change( );"> ... </form>If the starting input is a negative number,
then the text field's value is unnecessarily numberified via a
* 1 operationand the resulting number is subtracted from
0;this approach would work with positive inputs as well.
If the starting input is a positive number,
then a
- character is prepended to the text value;this approach would be problematic for a negative input in that, e.g.,
-5 would be converted to --5
and
eval("--5"), effected by clicking the key, would throw aSyntaxError: invalid decrement operand.
N.B. The ++ and -- operators cannot be used with numeric literal operands - see Stack Overflow's "Why can't we increment (++) or decrement (--) number literals" page - there is no discussion of this in Mozilla's Increment (++) and Decrement (--) documentation.
The former approach is semantically consistent with what we are trying to do, and we can fairly recast the
change( ) function as:function change( ) {
document.calculator.text.value = 0 - document.calculator.text.value; }Both
change( ) functions and the negpos( ) function are adequate for a numeric input, but what if we want to +/- a more complex expression?Parentheses and other interlopers, revisited
Back at the SC, suppose we type 2*(3+4) in the total field and it.
The
negpos( ) function returns NaN in this case because, as alluded to earlier, the presence of even one nonnumber operator character (let alone four such characters) in the initial obj.value kills the * (-1) multiplication.In contrast, Saries's calculator smoothly s 2*(3+4) to -2*(3+4) via the second if clause of the original
change( ) function;clicking the key then yields -14.
However, an attempted
0 - "2*(3+4)" subtraction with my revised change( ) function returns NaN.Now suppose we want to +/- 3+4.
For this case, the
negpos( ) and revised change( ) functions again return NaNwhereas the original
change( ) function returns -3+4,which is equally unacceptable as we want the return to
eval( ) to -7 rather than 1.We can circumvent these results in a hybrid way via:
/* For the change( ) function, var obj = document.calculator.text; */
if (isNaN(obj.value)) obj.value = "-(" + obj.value + ")";
else obj.value = 0 - obj.value;The if clause effectively parenthesizes the 3+4 input before prefixing it with a
-;
numeric inputs go through the else clause.Alternatively if not quite preferably, we can
eval( ) this type of input on the spot and subsequently subtract the eval( )ed value from 0:if (isNaN(obj.value)) obj.value = eval(obj.value);
obj.value = 0 - obj.value;This code takes 2*(3+4) to -14 and 3+4 to -7; it'll handle most mathematical expressions containing nonnumber characters (it'll take an entered Math.log(1024)/Math.log(2) to -10, e.g.) although it balks at the number1(number2) expressions that are generated by the else clause of the
more( ) function in collaboration with a number of other SC functions.Lagniappe: number1(number2) multiplication
Suppose we type 2 in the SC's total field.
We click the key and suddenly decide that we want to raise 3 to the 3rd power;
our final return is 2(27) when the
power( ) and more( ) functions have finished executing.A user who is conversant with basic mathematical conventions would understand the 2(27) expression as the multiplication of 2 and 27, but JavaScript doesn't see it that way. Attempted
eval( )uation of our 2(27) by clicking the key throws aTypeError: 2 is not a function.
(A function identifier can have one or more digits in it, but it can't just be a number.)
The Google calculator widget and the Calculator.net calculator will both carry out a number1(number2) multiplication, however, so maybe we should do that too. The retooled
calc( ) function below (cf. the original here) will get us there:function calc(obj) {
var mult_expr, exprArray;
mult_expr = /^([+-]?\d*\.?\d*)\(([+-]?\d*\.?\d*)\)$/;
if (! mult_expr.test(obj.value)) obj.value = eval(obj.value);
else {
exprArray = mult_expr.exec(obj.value);
if (exprArray[1]) obj.value = exprArray[1] * exprArray[2];
else obj.value = eval(obj.value); } }
<button type="button" onclick="calc(document.mainform.total);"> = </button>The mult_expr regular expression
var mult_expr = /^([+-]?\d*\.?\d*)\(([+-]?\d*\.?\d*)\)$/;matches a number1(number2) expression whose number1 and number2 numbers
may be signed with a + or a - (
[+-]?),have 0 or more integer digits (
\d*),may contain a decimal point (
\.?), andhave 0 or more fractional digits.
Noteworthily, the latter expression's decimal points, left parenthesis, and right parenthesis would normally be regexp metacharacters and must therefore be literalized with a backslash for the former expression.
Furthermore, the number1 and number2 zones in the mult_expr pattern are parenthesized so that we can remember them.
As detailed above, we can use the
test( ) method of the RegExp object to separate a normal number1*number2 multiplication from a number1(number2) multiplication.(f) For the former multiplication, the total value and the mult_expr pattern do not match and so
! mult_expr.test(obj.value) returns true, and the obj.value is accordingly eval( )ed as in the original calc( ) function.(l) For the latter multiplication, the total value and the mult_expr pattern do match and so
! mult_expr.test(obj.value) returns false; toward the end of getting our hands on the number1 and number2 numbers, the match is subsequently parsed via the exec( ) method of the RegExp object.Although we haven't made use of it previously, the
exec( ) method is analogous to the match( ) method of the String object, which we discussed in Blog Entry #222.The
mult_expr.exec(obj.value) call returns an array - let's call it exprArray - whose exprArray[1] and exprArray[2] elementshold the parenthesized substring matches for the number1 and number2 zones respectively and
can be multiplied to give us the product we want -
there, that wasn't so hard, was it, weekend silicon warriors?
The (3.141592653589793) string outputted by the SC's key also matches the mult_expr pattern; for this match, exprArray[1] holds the empty string, so the
exprArray[1] * exprArray[2] multiplication is shielded by an if (exprArray[1]) gateand an accompanying
else obj.value = eval(obj.value); clause takes (3.141592653589793) to 3.141592653589793.Another remembering
I was originally going to carry out the number1(number2) multiplication with a statement that calls on the $1 and $2 properties of the predefined RegExp object to remember the parenthesized substring matches of a
mult_expr.test(obj.value) match.if (mult_expr.test(obj.value))
obj.value = RegExp.$1 ? RegExp.$1 * RegExp.$2 : eval(obj.value);However, the RegExp.$1-$9 properties were deprecated as of JavaScript 1.5, and Mozilla warns,
These deprecated features can still be used, but should be used with caution because they are expected to be removed entirely sometime in the future. You should work to remove their use from your code.
Sounds like we should stick with the
exec( ) thing, wouldn't you say?The errors of
eval( )As intimated above, the attempted
eval( )uation of an inappropriate input throws an error of some sort. We can display the SC's eval( )-generated errors to the user (vs. letting them languish in the browser's debugging console) via a try...catch statement:try { /* calc( ) conditional code */ }
catch (err) { window.alert(err.name + ":\n" + err.message); }Your turn
Let's wrap things up with a little demo that illustrates the features presented in this section/post. Enter an expression -
+123.(-.456), -7*(8+9), Hello World!, whatever you want -
into the Expression field and then click the button.
We'll hit the SC's Memory functionality in the following entry.
Actually, reptile7's JavaScript blog is powered by Café La Llave. ;-)
