reptile7's JavaScript blog

Monday, May 30, 2016
Meet Me at the Quad, Part 2
Blog Entry #368
On the borders
The next CCC offering is "Perimeter of a Quadrilateral", which was authored by Sam S. Lachterman in late 1997. The Perimeter of a Quadrilateral script asks the user for the width and length of a quadrilateral and then plugs those values into a
var perimeter = (width * 2) + (length * 2); statement to give a perimeter, whose scope we will flesh out below.The Perimeter of a Quadrilateral script code is available here and (excepting its copyright comment) is reproduced below:
<head>
<script language="javascript">function perim( ) {
var width = window.prompt("Enter the width of the quadrilateral:", "");
var length = window.prompt("Enter the length of the quadrilateral:", "");
var perimeter = (width * 2) + (length * 2);
window.alert("The perimeter of the quadrilateral is " + perimeter + ". This was solved using the formula 2(l+w)."); }</script>
</head>
<body bgcolor="#ffffff" onload="perim( );">Quick comment on the alert( ) message: A
2(l+w) perimeter formula would require us to numberify the width and length, which would otherwise be concatenated and not added.var perimeter = 2 * (Number(length) + Number(width));Who's in and who's out
As quadrilateral types go, the (width * 2) + (length * 2) calculation duly applies to rectangles, and I guess we could say it applies to squares too, even as we would be stretching it to say that a square has a width and a length, but that's pretty much it.

(I recognize that length and width are standard terms for the dimensions of a rectangle, but they really don't sit well with me: working with CSS conditions me to prefer width for the horizontal distance and height for the vertical distance.)
A more general
(s1 * 2) + (s2 * 2) formulation could accommodate rhombuses, for which s1 and s2 are equal, and other parallelograms lacking right angles
and also kites for which
s1 ≠ s2.
The
(s1 * 2) + (s2 * 2) formula won't accommodate trapezoids and trapeziums, however.
Parallelograms, kites, and trapezoids are convex quadrilaterals, for which both diagonals lie inside the perimeter.
A quadrilateral can be concave: one diagonal is inside the perimeter and one diagonal is outside the perimeter.
A quadrilateral can be complex ("self-intersecting"): both diagonals are outside the perimeter.
(As you would intuit, a trapezium can be convex, concave, or complex.)

(s1 * 2) + (s2 * 2) works for some concave and complex quadrilaterals but not for others.The most general formula for calculating the perimeter of a quadrilateral,
perimeter = s1 + s2 + s3 + s4, simply adds up the lengths of all four sides, and is applicable to all quadrilaterals, without exception. So get out your rulers and get measuring, folks.You're so territorial
Sam also contributes a corresponding "Area of a Quadrilateral" script that asks the user for the width and length of a quadrilateral and then plugs those values into a
var times = (width * length); statement to give a(n) lw yea and nay
And how much mileage do we get with the width * length formula? Area = base × height is good for all parallelograms - close enough for government work, eh?

The gas runs out: width * length won't work for a kite that isn't a rhombus, for a trapezoid, or for any other kind of quadrilateral. As for a rhombus, we can get the area of a kite by multiplying the lengths of its diagonals and dividing the product by 2 (
d1 * d2 / 2).
We can get the area of a trapezoid by multiplying the average of its base lengths by its height.
There are a number of formulas for finding the area of a convex quadrilateral: Wikipedia catalogs them here. There is no general formula for finding the area of any quadrilateral although there is a general approach to doing so, namely,
(a) divide the quadrilateral into smaller shapes whose areas can be determined and then
(b) add up those areas.
Two Web videos that illustrate this approach are:
(1) Area of a quadrilateral on a grid from the Khan Academy
(2) Area of Complex Quadrilateral Figures from MissLichtle
We'll take up the next CCC script, "Another Great Science Calculator", in the following entry.
Wednesday, May 18, 2016
May the Circle Be Unbroken
Blog Entry #367
A couple of months ago we discussed an Areas script that calculates the areas of various two-dimensional geometric shapes. One of those shapes is a circle: upon inputting the radius of a circle, an areac( ) function determines the circle's area via a
var sum = radius * radius * pi; operation.The next Calendars, Clocks, and Calculators (CCC) script is "Circle Circumference", which was written by Sam S. Lachterman in late 1997. The Circle Circumference script should calculate the circumference of a circle from the circle's radius via a C = 2 × π × r equation; in practice, it plugs the radius into a
var circl = (radius * radius) * pi; statement to give the area.Code + brief deconstruction
Excepting the copyright comment in the
<head>, the Circle Circumference script code is reproduced below:<head>
<script language="javascript">function circle( ) {
var radius = window.prompt("Enter the radius of the circle:", "");
var pi = "3.141592654";
var circl = (radius * radius) * pi;
window.alert("The circumference of the circle is " + circl + ". This was solved using the formula (Rpi)(R)"; }</script>
</head>
<body bgcolor="#ffffff" onload="circle( );">When the script document has loaded, a circle( ) function springs into action. A prompt( ) box soliciting a circle radius immediately pops up. The user inputs a radius and clicks the button on the box and the input is assigned to a radius variable. The radius radius is squared and then the radius2 is multiplied by a toFixed(9) pi value and the resulting product is assigned to a circl variable. Finally, circl plus some supplementary text is displayed on an alert( ) box.
alert( ) formulae
Suppose for a moment that we do want the circle area and that we input a radius of 1 into the prompt( ) box. The alert( ) output will be:
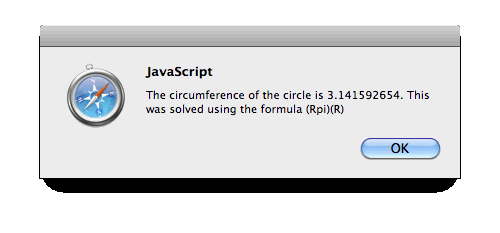
The (Rpi)(R) area formula leaves something to be desired, wouldn't you say? Much nicer would be:

window.alert("The area of the circle is " + area + ". This was solved using the formula: A = \u03c0 \u00d7 r\u00b2");Although neither π, ×, nor ² is an ASCII character, we can put all of them in an alert( ) message via their Unicode escape sequences. I find that FileFormat.Info is a useful site for tracking down these sequences; its pages for representing π, ×, and ² are here, here, and here, respectively: go to the "C/C++/Java source code" entry in the Encodings table(s) for the goods.
As for a circumference alert( ), I trust you can write that one out at this point.
Demo
The script demo at the Java Goodies radius.html page works as well as could be expected.
(a) The demo outputs a valid circle area if the prompt( ) input is a positive number.
(b) If the input is 0 or if the input field is left blank or if the button on the box is clicked, then the circl return is 0.
(c) A negative number input gives a positive circl - fair enough for an area calculation. If we were actually calculating the circumference, however, then a negative radius would give a negative circl, and that wouldn't make very much sense, now would it?
(d) If the input is a non-empty, non-numeric string (e.g., hello world), then circl is NaN.
Toward the end of getting the circumference I thought it appropriate to give you my own demo, so here we go:
Input
• The prompt( ) input interface is too 'in your face' for my taste: much better to get the radius via a text input.
<div id="circumferenceDiv">
...Heading, image, and equation, and/or other meta-information as you see fit...
<label>Enter the radius of the circle: <input type="text" id="radiusInput"></label>
• Trigger circle( ) - wait, let's call it getCircumference( ) - by clicking a push button.
function getCircumference( ) {
var radius = document.getElementById("radiusInput").value; ... }
<button type="button" onclick="getCircumference( );">Get the circumference</button>
• No pre-circl validation is provided for the user's input: unwanted numbers and strings should be turned away.
if (Number(radius) <= 0 || /\.\d{3,}$/.test(radius) || isNaN(radius) || radius === "") {
window.alert("Please enter a positive number with no more than two post-decimal point digits.");
document.getElementById("radiusInput").value = "";
document.getElementById("radiusInput").focus( );
return; }
No upper limit is set for the radius - you may want to calculate the circumference of Jupiter, after all.
• Use Math.PI in place of var pi = "3.141592654".
Output
• Calculate the circle circumference via a var circumference = 2 * Math.PI * radius; operation.
• Lose the alert( ) output. Truncate circumference at the hundredths place and then load it into a samp placeholder on the page.
document.getElementById("circumferenceSamp").textContent = circumference.toFixed(2);
The circumference of the circle is: <samp id="circumferenceSamp"></samp>
I/O
• Add a reset capability.
function resetCircumference( ) {
document.getElementById("radiusInput").value = "";
document.getElementById("circumferenceSamp").textContent = ""; }
<button type="button" onclick="resetCircumference( );">Reset</button>
</div>The next two CCC scripts respectively calculate the perimeter and area of a quadrilateral - we ought to be able to deal with both of them in one post.
Saturday, May 07, 2016
Paging Dr. Pythagoras
Blog Entry #366
OK, let's move on now to the next CCC script, "The Pythagorean Theorem". Authored by Greg Bland in early 1998, the Pythagorean Theorem script calculates the length of the hypotenuse (c) of a right triangle from the lengths of the other two sides (a and b) of the triangle via the equation a2 + b2 = c2.

The script demo at the aforelinked Java Goodies pythag.html page works fine as long as you input integers for the a and b lengths - more on this here. The Java Goodies pythag.txt document holding the script code is still live.
What we've got on the rendered page
<form name="pythagorean">
<center>
<p>The Pythagorean Theorem<br>
-Geometry's most elegant theorem-<i>a(squared) + b(squared) = c(squared)
<hr>
<p><input type="button" onclick="touse( );" value="To Use this....">
<p>a <input type="text" name="a" value="">
<p>b <input type="text" name="b" value="">
<p><input type="button" value="Compute.." onclick="solvepg( );">
<p>Output: <input type="text" name="theorem" value="">
</form></center>The user enters the a and b lengths into text inputs named a and b, respectively. Clicking a push button above the a field calls a touse( ) function that displays a help message on an alert( ) box. Clicking a push button below the b field calls a solvepg( ) function that determines the c length and loads it into a text input named theorem.
a
b
Output:
A name="pythagorean" form contains the input fields and buttons; a center element horizontally centers the display. As shown, the form and center elements overlap, and they shouldn't do that.
The pythagorean form is prefaced with a header:
The Pythagorean Theorem
-Geometry's most elegant theorem- a(squared) + b(squared) = c(squared)
The a(squared) + b(squared) = c(squared) equation is italicized by an i element whose required
</i> tag is missing. The italicization propagates to the a, b, and Output: field labels even though the i element has an (%inline;)* content model; you'd expect the browser to close the i element when it hits the %block; hr element but that doesn't happen.Also regarding the equation, there's no need to write out (squared) when we can specify the squaring operations with superscripted 2s, e.g.,
a<sup>2</sup>.Solve it
function solvepg( ) {
a = document.pythagorean;
b = a.a.value;
c = a.b.value;
c = parseInt(c);
b = parseInt(b);
b = b * b;
c = c * c;
d = b + c;
e = Math.sqrt(d);
document.pythagorean.theorem.value = e; }The solvepg( ) function first gives the pythagorean form an a identifier. The values of the a and b fields of the a form are then assigned respectively to b and c variables. (The a.a and a.b reference expressions don't cause any problems, in case you were wondering.) The b and c strings are subsequently numberified with the parseInt( ) function.
Next, the b and c numbers are squared; b2 is assigned back to b and c2 is assigned back to c. The b and c squares are added: the sum is stored in a d variable. A Math.sqrt( ) operation takes the square root of d: the root is stored in an e variable. Finally, e is assigned to the value of the theorem field.
The parseInt( ) blues
If the a and b user inputs are floating-point numbers, then the parseInt( ) operations will effectively Math.floor( ) those numbers, and we don't want to do that. Consider the 3:4:5 right triangle. If the a input is 2.999 and the b input is 3.999, then the parseInt( ) floorings lead to e = 3.605551275463989 (√13) - not good. It's actually not necessary to explicitly numberify the a.a and a.b values as the attempted multiplication of two numeric strings gives the hoped-for product, although you could appropriately Number( ) them if you feel that doing so improves the code's readability.
Oh yeah...
The touse( ) function is:
function touse( ) {
window.alert("Just enter a and b, don't square [them], your computer will do it for you."); }I think that'll do it for our discussion of the Pythagorean Theorem script. I suppose at this point I could go through some additional changes I would make to the script's HTML (e.g., lose the
<form>, convert the <center> to a <div>) and JavaScript (e.g., add a validation conditional that intercepts unwanted number/string inputs, truncate es that run many places past the decimal point) and roll out my own demo, but I trust that you yourself are up to the task of doing those things. Looking forward, then, the next CCC script is "Circle Circumference", and we'll check it out in our next episode.Actually, reptile7's JavaScript blog is powered by Café La Llave. ;-)

