Saturday, February 28, 2015
Real to Irreal
Blog Entry #344
In today's post, we'll make some additional changes to the JavaScript Goodies Quadratic Equation script and then roll out a demo that incorporates those changes.
Process it
In the original script, the equation-solving process( ) function is called by changing the value of the Variable c field. The onchange trigger isn't intuitive enough for my taste: I would much rather click a button.
<tr><td><button class="button" type="button" onclick="process( );">Solve for x</button></td></tr>Input validation
I find that the simplest and smoothest approach to validating the Variable a/b/c values is to carry out all of the
"invalid number" tests at the beginning of the process( ) function vis-à-vis flagging non-number inputs as we go along as is done in the original script.function process( ) {
var a = document.qform.a, b = document.qform.b, c = document.qform.c;
if (a.value == 0 && a.value !== "") {
window.alert("Didn't we tell you that the 'a' coefficient can't be 0?");
a.value = ""; a.focus( ); return; }
if (isNaN(a.value) || a.value === "") { // Recall that isNaN("") returns false.
window.alert("Your 'a' input must be a number.");
a.value = ""; a.focus( ); return; }
if (isNaN(b.value) || b.value === "") {
window.alert("Your 'b' input must be a number.");
b.value = ""; b.focus( ); return; }
if (isNaN(c.value) || c.value === "") {
window.alert("Your 'c' input must be a number.");
c.value = ""; c.focus( ); return; }
/* ...Equation-solving code... */ }• The first if statement stops us from entering 0 into the Variable a field well before we get to the 'divide by 2a' stage. As the
0 == "" comparison returns true, a a.value !== "" subcondition is necessary to distinguish a 0 input from simply leaving the Variable a field blank.• The remaining if statements flag all non-number values: these tests can also be carried out via a regular expression, e.g.,
if (!/^-?\d{1,3}(\.\d{1,2})?$/.test(a.value)) { ... }, but the isNaN( ) function plus an identity operation is a more straightforward way to go, yes?• In practice, the above code clears the first invalid field and gives focus to that field, whereas the original script's over( ) function heavy-handedly clears all of the fields and always returns focus to the Variable a field.
• Each if statement is equipped with a
return that effectively stops the browser from barreling on to the equation-solving part of the code.All those digits
As shown in the previous post, the process( ) function's plus / den and minus / den divisions return roots that can run as many as 16 places past the decimal point, and you probably don't want that. We can easily cut most of those digits loose via the Number object's toFixed( ) method or toPrecision( ) method, e.g.:
plus = plus / den;
if (/\.\d{4,}$/.test(plus)) plus = plus.toFixed(3);
minus = minus / den;
if (/\.\d{4,}$/.test(minus)) minus = minus.toFixed(3);The above snippet uses a
\.\d{4,}$ regular expression to flag plus and minus quotients that run more than 3 places past the decimal point and a toFixed(3) operation to chop off the post-thousandths digits of such quotients; other pluses and minuses, be they integers or floating-point numbers, are left alone.It's complex
Consider the equation x2 + x + 1 = 0, for which b2 - 4ac is -3: as noted last time, the process( ) function pops up a "The solution is NO SOLUTION" message for such an equation. (If you graph y = x2 + x + 1, you'll see that the resulting parabola 'bottoms out' above the x-axis at (-½, ¾).)
Of course, there's nothing forcing us to stay within the real number system, and it is not at all difficult to produce complex roots for quadratic equations that do not have real roots.
a = a.value; b = b.value; c = c.value;
var num = b * b - 4 * a * c;
var den = a * 2;if (num < 0) {
var quot1 = -b / den;
if (/\.\d{4,}$/.test(quot1)) quot1 = quot1.toFixed(3);
num = Math.sqrt(-num);
var quot2 = num / den;
if (/\.\d{4,}$/.test(quot2)) quot2 = quot2.toFixed(3);
var plus = quot1 + " + i \u00D7 " + quot2; // \u00D7 encodes the × symbol.
var minus = quot1 + " - i \u00D7 " + quot2; }
else { /* ...If the roots are real... */ }For x2 + x + 1 = 0, this gives:
plus = -0.5 + i × 0.866
minus = -0.5 - i × 0.866
I trust you're up to the task of formatting the plus and minus strings differently if you want to do that.
A streamlined reset
function over( ) { document.qform.reset( ); document.qform.a.focus( ); }'Nuff said.
Not mentioned previously
The quad.html document head contains two IE-only "meta transitions":
<meta http-equiv="Page-Enter" content="RevealTrans (Duration=2, Transition=23)">
<meta http-equiv="Page-Exit" content="RevealTrans (Duration=3, Transition=23)">This code has nothing to do with quadratic equations and is in any case
effectively obsoleteaccording to this page: throw it out.
Final editing
For my demo below, I
(a) trade in the white/#2574d5-on-black color scheme for a classic black-on-white color scheme,
(b) left-justify the intro, quadratic.jpg image, and qtable table,
(c) remove the
<hr width="275"> between the display heading and the rest of the intro, (d) get rid of all of those *pt font-sizes,
(e) put each field and its label in the same row/cell, and
(f) park the plus and minus strings in separate Root #1 and Root #2 fields.
There, we're all set. Go get your favorite quadratic equation and let's get solving, shall we?
Demo
~ ~ Quadratic Equation Script * * . . .
To take full advantage of this script, please read the following explanation.The equation you are trying to solve is: ax2 + bx + c = 0, which is a quadratic equation, more specifically, the equation used to find the x-intercepts, if any, of a parabola.
The 'a' coefficient cannot equal zero.
This is the form of the solution set for the quadratic equation:
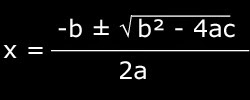
Actually, reptile7's JavaScript blog is powered by Café La Llave. ;-)

